 Four
Four
 Four
Four
4 is a number, a word or symbol used to designate quantities or, by extension, entities having quantitylike properties.
Rational NumbersThe simplest numbers are the natural numbers, 1, 2, 3, ..., used in counting; they are also called the whole numbers, positive integers, or positive rational integers. The natural numbers are closed with respect to addition and multiplication; that is, the sum and product of two natural numbers are always natural numbers. Because the quotient of two natural numbers, however, is not always a natural number, it is convenient to introduce the positive fractions to represent the quotient of any two natural numbers. The natural number n is identified with the fraction n/1. Furthermore, because the difference of two positive fractions is not always a positive fraction, it is expeditious to introduce the negative fractions (including the negative integers) and the number zero (0). The positive and negative integers and fractions, and the number 0, comprise the rational number system.
The sum, difference, product, or quotient of two rational numbers is
always a rational number. Division of any number by zero, however, is
not allowed. It can be shown that every rational number can be
represented as a repeating or periodic decimal, that is, as a number
in the decimal notation, which after a certain point consists of the
infinite repetition of a finite block of digits. Conversely, every
repeating decimal represents a rational number. Thus, 617/50 =
12.34000 ..., and 2317/990 = 2.34040 ... The first expression is
usually written as 12.34, omitting the infinite repetition of the
block consisting of the single digit 0. The second expression is
frequently written as
Irrational NumbersThe development of geometry indicated the need for more numbers; the length of the diagonal of a square with sides one unit long cannot be expressed as a rational number. Similarly, the ratio of the circumference to the diameter of a circle is not a rational number. These and other needs led to the introduction of the irrational numbers. A decimal expansion that is neither of the two types described above represents an irrational number. For example,
Imaginary NumbersThe product of a real number multiplied by itself is 0 or positive; the equation x = -1 has no solutions in the real
number system. If such a solution is desired, new numbers must be
invented. Let i = = -1 has no solutions in the real
number system. If such a solution is desired, new numbers must be
invented. Let i =
 Imaginary numbers (the term must not be used in a literal sense but in the technical sense just described) are extremely useful in the theory of alternating currents and many other branches of physics and natural science.
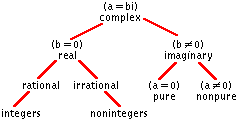
Complex NumbersIn 1799 the German mathematician Carl Friedrich Gauss proved that every algebraic equation of degree n having the form x + a + a x x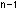 + ... +
a + ... +
a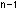 k k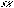 +
a +
a = 0 in which a = 0 in which a ,
a ,
a ..., a ..., a are arbitrary
complex numbers, is satisfied by at least one complex root. are arbitrary
complex numbers, is satisfied by at least one complex root.
Whereas real numbers represent points on a line, complex numbers can be placed in correspondence with the points on a plane. To represent the complex number a + bi geometrically, the x-axis is used as the axis of the real number a, and the y-axis serves as the axis of the pure imaginary bi; the complex number, therefore, corresponds to the point P with the rectangular coordinates a and b. The line, or vector, joining the origin with the point P (a,b) is the diagonal of a rectangle with the sides a and bi.
If the complex number a + bi is multiplied by -1, the vector OP is
rotated through 180 degrees, and the point P falls in the third
quadrant; a rotation of 90 degrees, therefore, represents
multiplication of the complex number by i, as -1 = 1
Mystical and magical qualities have been ascribed to numbers both in
antiquity and in modern times. The pseudoscience of numerology
attempts to interpret the occult by means of the symbolism of
numbers, which is based on the Pythagorean doctrine that all things
are numbers and consist of geometrical figures in various patterns.
|